Data Structures and Algorithms (DSA) are the fundamental concepts in computer science and programming. Data structures organise and store data, while algorithms provide the procedures to process and manipulate that data. Together, they enable software development to solve several problems and tasks across various domains. They reduce the number of lines of code when solving complex code. The knowledge of DSA aids in completing code with reduced space and time complexity. Thus, its usage in coding aids in cracking the highest-paying job interviews. Some are a few DSA concepts to help you ace the coding round:
1. Arrays
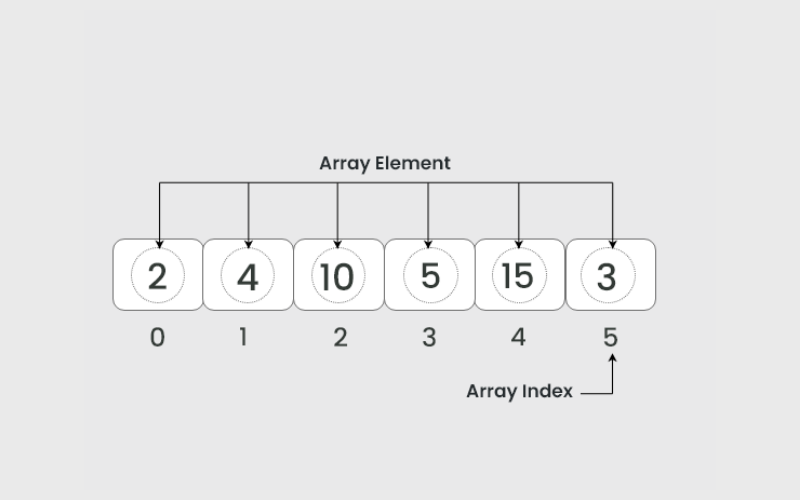
Arrays are the most superficial and most used data structures. They store a collection of elements of a similar data type in contiguous memory space. Each element is managed by an index, making array access very fast. However, it has a fixed size, so they can’t handle dynamic data changes.
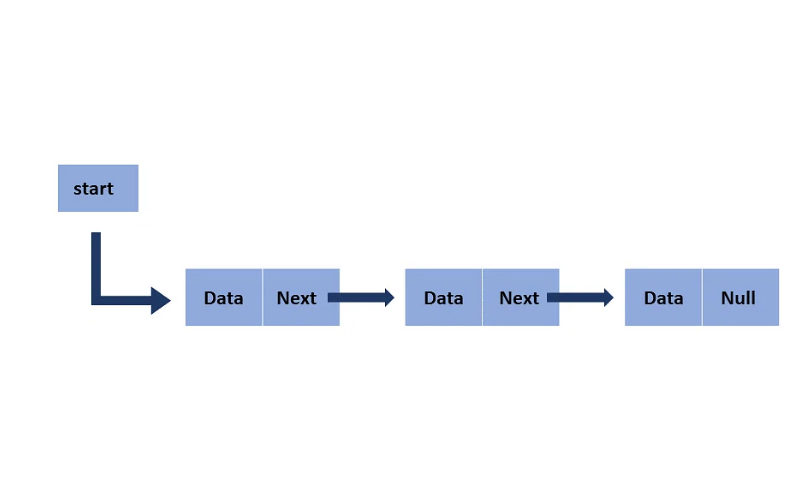
2. Linked Lists
Linked lists are linear data structures containing nodes, where each node has data and a reference (or link) to the next node. This structure permits dynamic memory allocation and efficient insertions and deletions, as nodes are rearranged easily. However, accessing elements by index is slower than arrays, as you must traverse the list from the beginning.
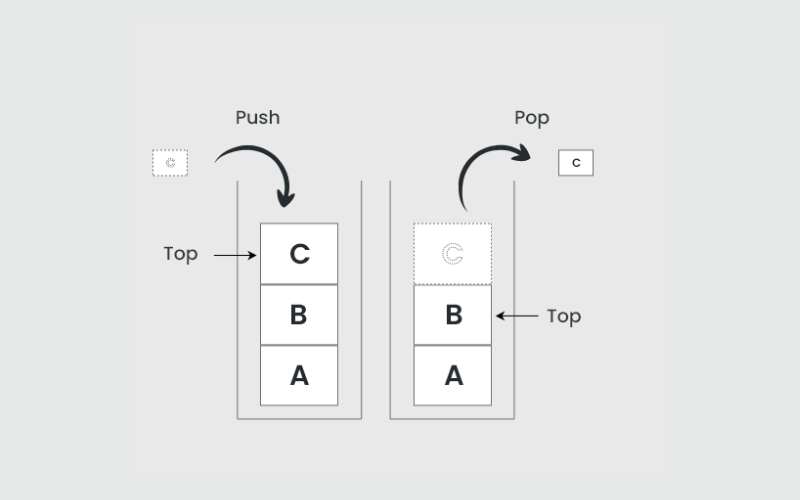
3. Stacks
Stacks are linear data structures following the Last-In-First-Out (LIFO) principle. Elements can be added and removed from the same end, called the top. They manage function calls, track state changes, and solve problems involving recursive algorithms.
4. Queues
Queues are linear data structures based on the First-In-First-Out (FIFO) principle. Elements added at the rear called enqueue and removed from the front called dequeue. Queues are essential for scheduling processes, managing resources, and implementing breadth-first search algorithms.

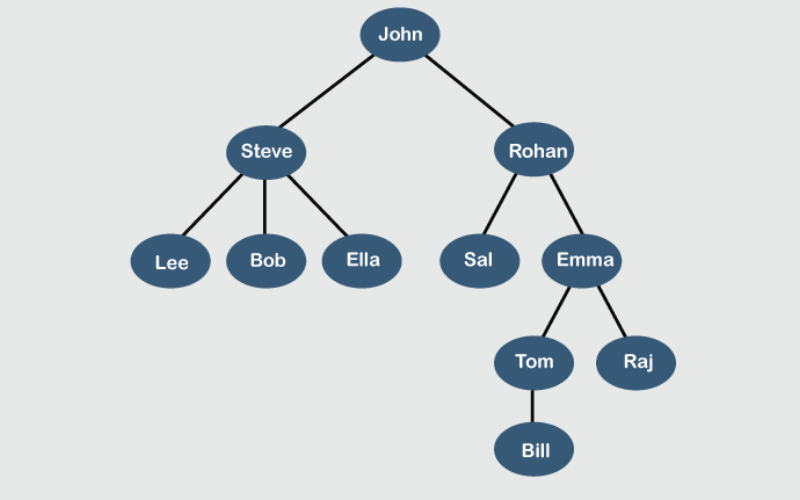
5. Trees
Trees are hierarchical data structures having a root node that has child nodes. Trees are versatile and represent relationships (e.g., family trees), organise hierarchical data (e.g., file systems), and implement advanced data structures like heaps and search trees.
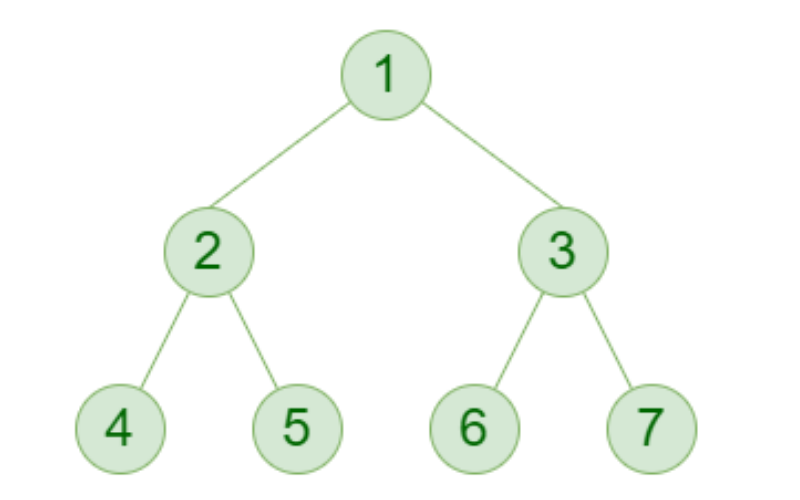
6. Binary Trees
Binary trees are trees where each node has at most two children: a left child and a right child. They are used for binary search trees and expression evaluation (e.g., parsing arithmetic expressions).
7. Binary Search Trees (BST)
BSTs are binary trees with a specific ordering property: for each node, all nodes in its left subtree have values less than the node’s value, and all nodes in its right subtree have values greater. This property aids in efficient searching, insertion, and deletion operations.
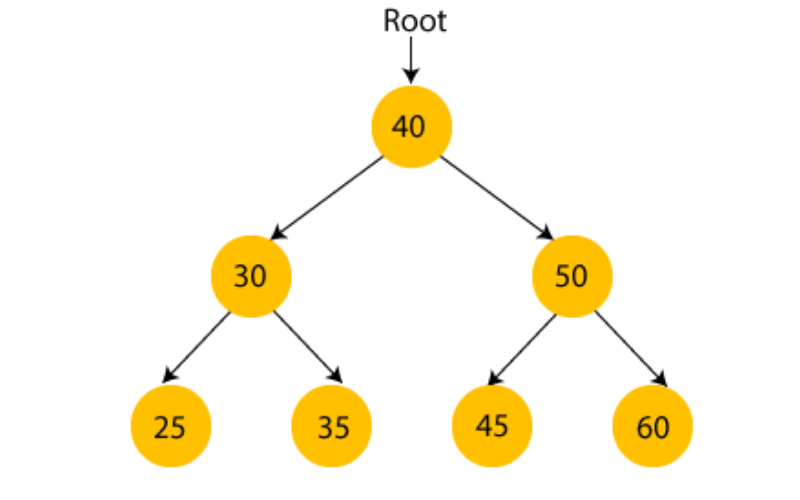
8. Heaps
Heaps are tree-based data structures ensuring the lowest (min-heap) or highest (max-heap) element is at the root. Both max-heaps and min-heaps have the heap property, ensuring that every parent node sticks to the specified comparison rule (greater than or less than its children). It is for sorting algorithms like heapsort and priority queues.
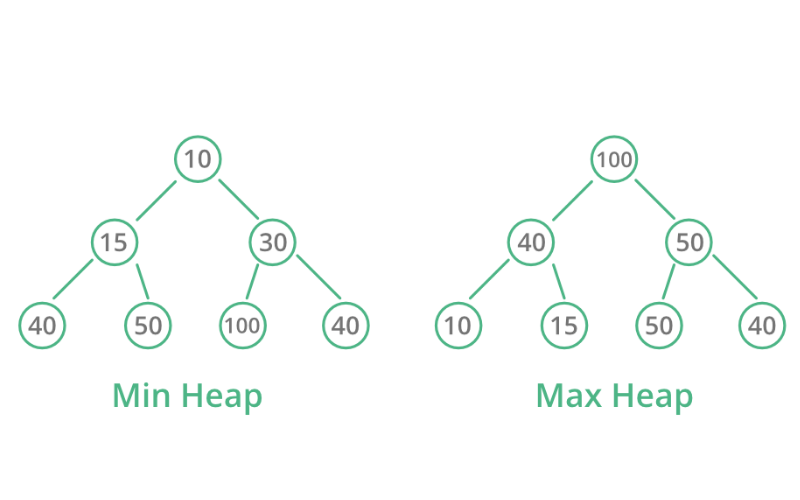
9. Hashing
Hashing involves mapping data (keys) to fixed-size arrays (buckets) using a hash function. The hash function is a mathematical procedure that converts one input numeric value into another. Hash tables are implemented for efficient data retrieval and storage functionalities, making them essential for dictionary-like structures and databases.
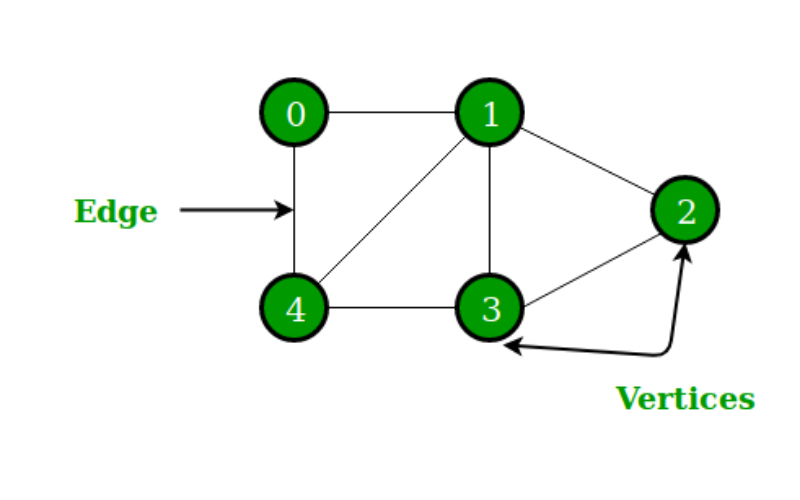
10. Graphs
A graph is a versatile data structure that consists of nodes (vertices) connected by edges. These edges can have various properties, including direction (directed or undirected) and weight (weighted or unweighted). Graphs find applications in several domains, such as network routing, social network analysis, and recommendation systems.
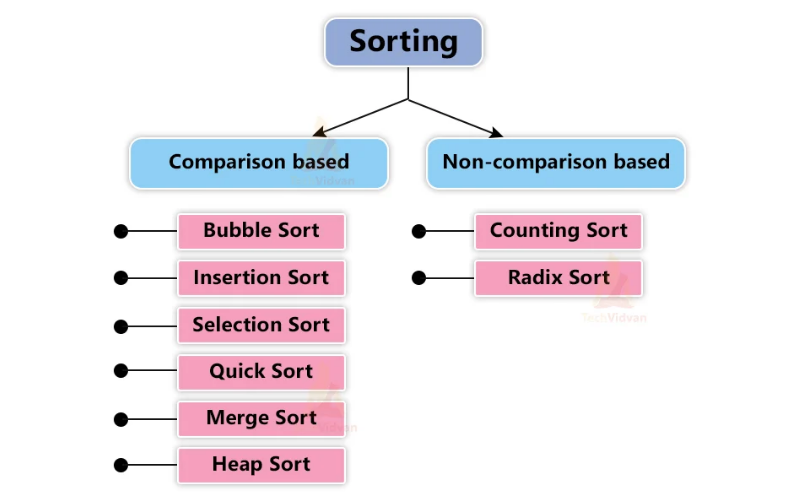
11. Sorting Algorithms
Sorting algorithms arrange a list of elements in a particular order. There are various sorting algorithms, including Selection Sort, Insertion Sort, Bubble Sort, Merge Sort, and Quick Sort. Each algorithm has its space and time complexity characteristics, making them apt for different scenarios.
12. Trie
A trie is a tree-like data structure used for storing and searching strings. It’s handy for tasks like autocomplete, spell-checking, and IP routing tables. They have a branching factor equal to the size of the alphabet and provide quick string retrieval.
13. Segment Trees
Segment trees are hierarchical data structures used for various range-query tasks, such as finding the sum or minimum/maximum value within a specified range in an array. They are prevalent in competitive programming and help solve problems involving intervals or segments.
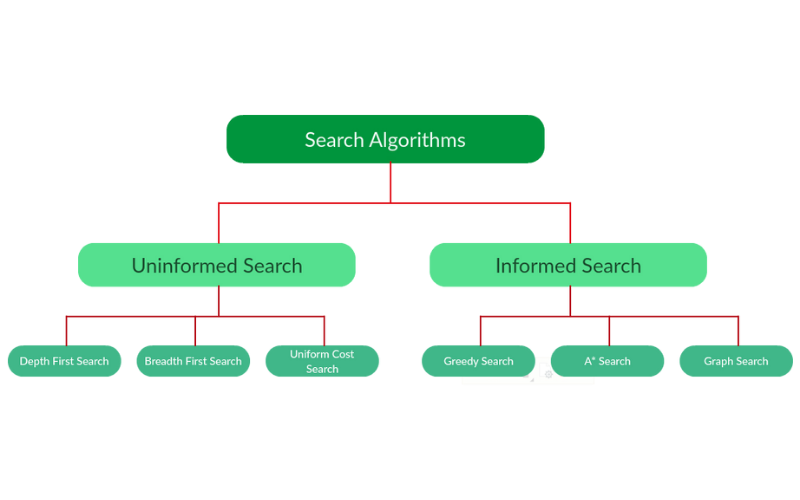
14. Searching Algorithms
Searching algorithms locate specific elements or values in a data structure. Standard searching algorithms include Binary Search, Linear Search, Depth-First Search (DFS), and Breadth-First Search (BFS). They are involved in tasks like information retrieval and graph traversal.
15. Greedy Algorithms
Greedy algorithms make a series of locally optimal choices at each step to arrive at a globally optimal solution. They are efficient and straightforward to implement but may not produce the best results. Examples include Dijkstra’s algorithm for shortest paths and Huffman coding for data compression.
16. Backtracking
Backtracking is a technique for solving problems incrementally by trying different possibilities and undoing them if they don’t lead to a valid solution. It is for solving puzzles (e.g., Sudoku), generating permutations, and solving the N-Queens problem.
![]()
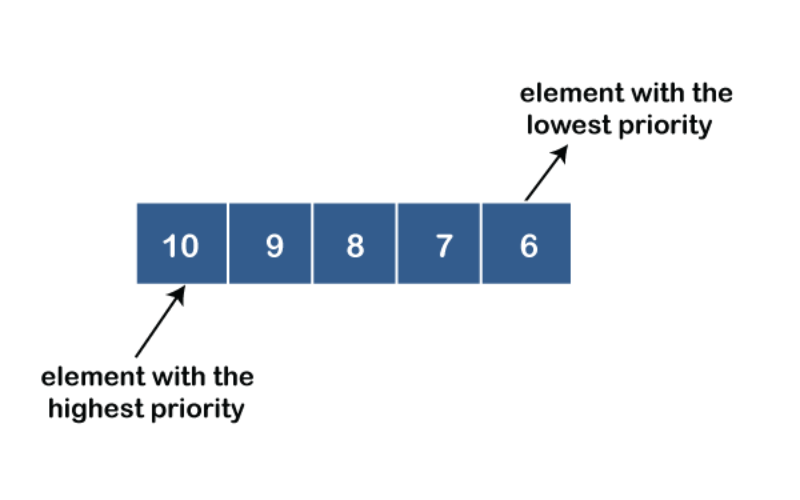
17. Priority Queues
A priority queue is a data structure that maintains a set of elements with associated priorities. It permits efficient insertion and removal of the element with the highest priority. They are involved in algorithms like Dijkstra’s shortest path and A* search.
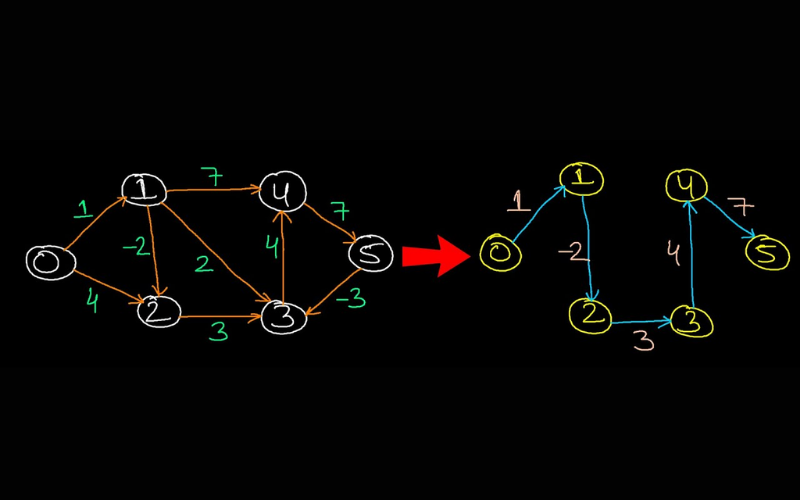
18. Bellman-Ford Algorithm
Bellman-Ford algorithm is a dynamic programming-based algorithm for determining the shortest path from a source vertex to other vertices in a directed, weighted graph. It deals with graphs having negative weight edges as long as there are no negative weight cycles. It is helpful in scenarios, including network routing and detecting negative weight cycles.
19. Topological Sorting
Topological sorting is an algorithm used to linearly order the vertices of a directed acyclic graph (DAG) so that for every directed edge, vertex u comes before vertex v in the ordering. This ordering is displayed as a sequence or a list. It finds its extensive use in tasks like scheduling jobs with dependencies and solving compiler constraints.
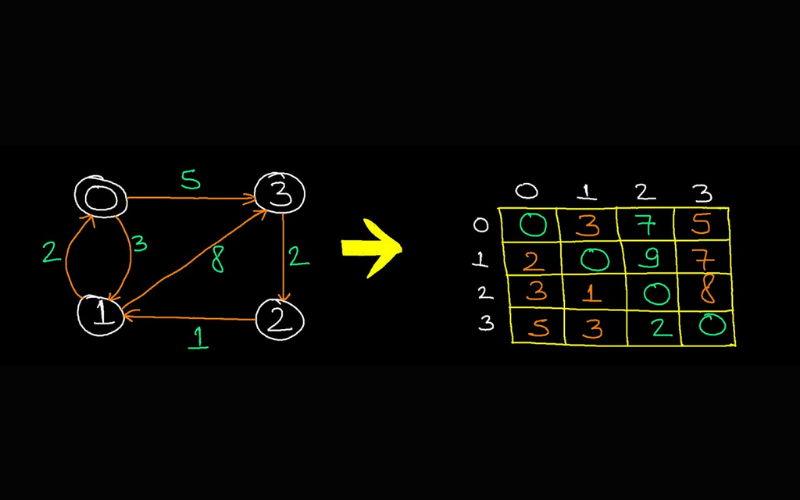
20. Floyd-Warshall Algorithm
Floyd-Warshall algorithm finds the shortest paths for all pairs of vertices in a weighted, directed graph. It is versatile and can handle graphs with positive and negative edge weights and detect negative weight cycles. It is used in network routing and applications where the shortest path of all pairs of nodes is needed, as in Geographical Information Systems (GIS).